En la actualidad, el álgebra de Boole se aplica de forma generalizada en el ámbito del diseño electrónico. Claude Shannon fue el primero en aplicarla en el diseño de circuitos de conmutación eléctrica biestables, en 1948. Esta lógica se puede aplicar a dos campos:
- Al análisis, porque es una forma concreta de describir como funcionan los circuitos.
- Al diseño, ya que teniendo una función aplicamos dicha álgebra, para poder desarrollar una implementación de la función
¿QUE ES EL ÁLGEBRA BOOLEANA?
El álgebra booleana es un sistema matemático deductivo centrado en los valores cero y uno (falso y verdadero). Un operador binario " 0 " definido en éste juego de valores acepta un par de entradas y produce un solo valor booleano, por ejemplo, el operador booleano AND acepta dos entradas booleanas y produce una sola salida booleana.
Sea B un conjunto en el cual se definen dos operaciones binarias, + y *, y una
operación unitaria denotada ; sean 0 y 1 dos elementos diferentes de B. Entonces la
sextupla:
〈B, +, *, , 0, 1〉
se denomina álgebra de Boole si se cumplen los siguientes axiomas para cualesquiera
elementos a, b, c del conjunto B:
[B1] Conmutatividad:
(1a) a + b = b + a (1b) a * b = b * a
[B2] Distributividad:
(2a) a + (b * c) = (a + b) * (a + c) (2b) a * (b + c) = (a * b) + (a * c)
[B3] Identidad:
(3a) a + 0 = a (3b) a * 1 = a
[B4] Complemento:
(4a) a + a = 1 (4b) a * a = 0
¿Para que se utiliza?
Para tratar expresiones de la lógica proposicional para así poder solucionar mas rápidamente problemas como lo son los que tiene que ver con el ámbito de diseño electrónico.Y hubo algunas personas las cuales usaban estas teorías para aplicarlas en el diseño de circuitos de conmutación eléctrica como fue “Claude Shannon”.
De la misma manera en nuestra actualidad se le ha dado un uso directo: en la electrónica,durante el análisis de los circuitos electrónicos:
Lógica: la cual trabajan con señales electrónicas.
Digital: es mas usado en la computación ya que maneja señales electrónicas discretas.
Formas Canónicas
A partir de una tabla de verdad es posible obtener múltiples expresiones para la misma función, y todas estas expresiones son equivalentes entre ellas.
¿Que es un maxitermino?
Primera Forma Canónica
La primera forma canónica está formada por la suma de productos (minitérminos) y se desarrolla tomando la tabla de verdad y eligiendo las combinaciones de entradas en las que la salida se hace 1 y descartando las que son igual a 0.
¿Que es un minitermino?
Segunda Forma Canónica
La segunda forma canónica está formada por el producto de sumas (maxitérminos) y se desarrolla tomando la tabla de verdad y eligiendo las combinaciones de entradas en las que la salida se hace 0 y descartando las que son igual a 1.
¿Que es un circuito?
Un circuito lógico es un dispositivo que tienen una o más entradas y exactamente una salida. En cada instante cada entrada tiene un valor, 0 o 1; estos datos son procesados por el circuito para dar un valor en su salida, 0 o 1. Los valores 0 y 1 pueden representar ciertas situaciones físicas como, por ejemplo, un voltaje nulo y no nulo en un conductor.
Los circuitos lógicos se construyen a partir de ciertos circuitos elementales denominados compuertas lógicas, entre las cuales diferenciaremos:
• Compuertas lógicas básicas: OR, AND, NOT.
• Compuertas lógicas derivadas: NOR, NAND.
¿Que son las compuertas lógicas?
Los circuitos digitales (lógicos) operan en el modo binario donde cada voltaje de entrada y salida es un 0 o un 1; las designaciones 0 y 1 representan rangos de voltaje predefinidos.
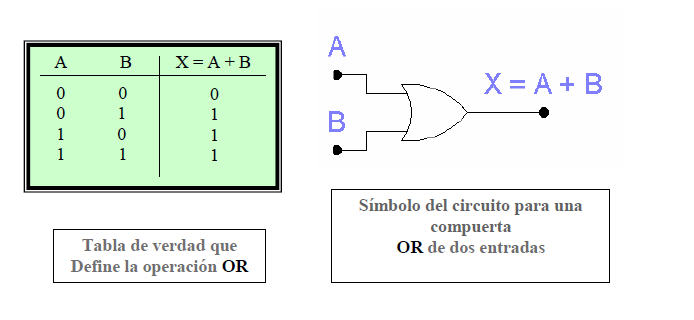
Operación OR con compuertas OR
la operación OR es la primera de las tres operaciones booleanas básicas que se debe aprender.
La expresión booleana para la operación OR es:
X = A + B
En esta expresión, el signo + no representa la adición común, sino la operación OR (lógica), entonces tendríamos 1 + 1 = 1.
Operación AND con compuertas AND
La operación AND es la segunda operación básica booleana, la expresión booleana para la operación AND es:
X = A . B
En esta expresión el signo (.) representa la operación booleana AND y no la multiplicación.
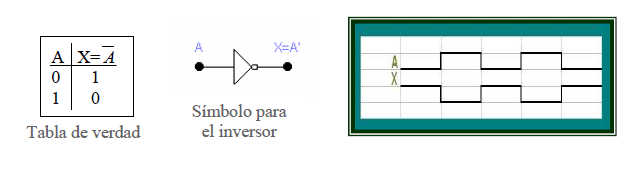
Operación NOT
La operación NOT difiere de las operaciones OR y AND en que se pueden realizar en una sola variable de entrada. Por ejemplo, si la variable A se somete a la operación NOT, el resultado X se puede expresar como:
X= A.





No hay comentarios:
Publicar un comentario